【題目描述】

（1）圖的深度優先搜索演示。

專業領域包括網站設計、做網站、購物商城網站建設、微信營銷、系統平臺開發， 與其他網站設計及系統開發公司不同，創新互聯的整合解決方案結合了幫做網絡品牌建設經驗和互聯網整合營銷的理念，并將策略和執行緊密結合，為客戶提供全網互聯網整合方案。

要求：圖采用鄰接表存儲結構，編程實現圖的創建、圖的深度優先搜索遞歸算法。 ???????

（2）圖的廣度優先搜索演示。

要求：圖采用鄰接表存儲結構，編程實現圖的創建、圖的深度優先搜索遞歸算法。

（3）求帶權無向圖的最小生成樹問題。

（4）求帶權有向圖中從某個源點出發到其余各頂點的最短路徑問題。

【代碼實現】

廢話不多說直接上代碼

#include#includeusing namespace std;
#define MVNum 100//大的頂點數
#define Max 1000//沒有權值時的∞
//邊節點
typedef struct ArcNode {
	int adjvex;//該邊所指向的頂點的位置
	ArcNode* nextarc;//指向下一條邊的指針
	int info;//邊的權值
};
//點節點
typedef struct VNode {
	char data;//頂點信息
	ArcNode* firstarc;//指向第一條依附該頂點的邊的指針
};
//鄰接表
typedef struct ALGragh {
	VNode vertices[MVNum];//頂點數組
	int visited[MVNum];//標志數組
	int vexnum, arcnum;//圖當前頂點數和邊數
};
//輔助數組的定義，用來記錄從頂點集U到V-U的權值最小的邊
typedef struct closeEdge {
	int adjvex;//最小邊在U中的那個頂點
	int lowcost;//最小邊的權值
};
//通過點的信息定位點的位置
int LocateVex(ALGragh G, char c) {
	for (int i = 0; i< G.vexnum; i++) {
		if (G.vertices[i].data == c) {
			return i;
		}
	}
}
//將標志數組歸零，每次深度遍歷圖之后都要歸零
void reZero(ALGragh &G) {
	for (int i = 0; i< G.vexnum; i++)	
		G.visited[i] = 0;
}
//鄰接表創建帶權無向圖(undirected graph)
void CreateUDG(ALGragh& G) {
	cout<< "請輸入圖的頂點數和邊數:";
	cin >>G.vexnum >>G.arcnum;
	cout<< "請依次輸入各頂點信息(以空格分割):";
	for (int i = 0; i< G.vexnum; i++) {
		cin >>G.vertices[i].data;
		G.visited[i] = 0;//將標志數組初始化為0
		G.vertices[i].firstarc = NULL;
	}
	char v1, v2;
	int info;
	for (int k = 0; k< G.arcnum; k++) {
		cout<< "請輸入一條邊的兩個頂點信息和邊的權值:";
		cin >>v1 >>v2 >>info;
		//確定v1和v2在G中的位置
		int i = LocateVex(G, v1); int j = LocateVex(G, v2);
		//分別將頂點v1和v2指向該條邊
		ArcNode *p1 = new ArcNode;//生成一個新的邊節點
		p1->adjvex = j; p1->info = info;
		p1->nextarc = G.vertices[i].firstarc;
		G.vertices[i].firstarc = p1;
		ArcNode* p2 = new ArcNode;
		p2->adjvex = i; p2->info = info;
		p2->nextarc = G.vertices[j].firstarc;
		G.vertices[j].firstarc = p2;
	}
}
//鄰接表創建帶權有向圖(undirected graph)
void CreateDG(ALGragh& G) {
	cout<< "請輸入圖的頂點數和邊數:";
	cin >>G.vexnum >>G.arcnum;
	cout<< "請依次輸入各頂點信息(以空格分割):";
	for (int i = 0; i< G.vexnum; i++) {
		cin >>G.vertices[i].data;
		G.visited[i] = 0;//將標志數組初始化為0
		G.vertices[i].firstarc = NULL;
	}
	char v1, v2;
	int info;
	for (int k = 0; k< G.arcnum; k++) {
		cout<< "請輸入一條邊的兩個頂點信息和邊的權值:";
		cin >>v1 >>v2 >>info;
		//確定v1和v2在G中的位置
		int i = LocateVex(G, v1); int j = LocateVex(G, v2);
		//有向圖只需將v1連接該條邊
		ArcNode* p1 = new ArcNode;//生成一個新的邊節點
		p1->adjvex = j; p1->info = info;
		p1->nextarc = G.vertices[i].firstarc;
		G.vertices[i].firstarc = p1;
	}
}
//圖的深度優先遍歷
void DFS(ALGragh &G,char v) {
	cout<< v; G.visited[LocateVex(G,v)] = 1;//將訪問過的標志數組設為1
	ArcNode *p = G.vertices[LocateVex(G,v)].firstarc;//p指向v的邊鏈表的第一個邊節點
	while (p != NULL) {
		int w = p->adjvex;//w是v的鄰接點
		//如果w未訪問，則繼續遞歸
		if (!G.visited[w])	DFS(G, G.vertices[w].data);
		p = p->nextarc;//否則繼續深入
	}
}
//圖的廣度優先遍歷
void BFS(ALGragh G, char v) {
	cout<< v; G.visited[LocateVex(G, v)] = 1;
	queueQ;
	Q.push(v);//v入隊
	while (!Q.empty()) {
		char u = Q.front(); Q.pop();//隊首出隊
		ArcNode* p = G.vertices[LocateVex(G, u)].firstarc;
		while (p != NULL) {
			int w = p->adjvex;
			if (!G.visited[w]) {
				cout<< G.vertices[w].data;//如果w未訪問，則輸出該節點
				G.visited[w] = 1;
				Q.push(G.vertices[w].data);//入隊
			}
			p = p->nextarc;
		}
	}
}
//查找輔助數組的V-U中，邊的最小值
int Min(closeEdge c[],int num) {
	int min = Max;//記錄最小邊的權值
	int flag = 0;//記錄最小邊所在頂點
	for (int i = 0; iadjvex].lowcost = p->info;
		p = p->nextarc;
	}
	//prim
	for (int i = 0; i< G.vexnum - 1; i++) {
		k = Min(ce,G.vexnum);
		int u0 = ce[k].adjvex;//最小邊的頂點
		cout<< G.vertices[u0].data<< " "<< G.vertices[k].data<< " 權值:"<< ce[k].lowcost<< endl;
		ce[k].lowcost = 0;//將第k個頂點并入U集
		//新頂點并入U后重新選擇最小邊
		p = G.vertices[k].firstarc;
		while (p != NULL) {
			for (int j = 0; j< G.vexnum; j++)
				if (p->info< ce[j].lowcost && j == p->adjvex)
					ce[j] = { k,p->info };
			p = p->nextarc;
		}
	}
}
//用dijkstra算法求最短路徑
void ShortestPath_Dijkstra(ALGragh G,char a) {
	bool S[MVNum];//記錄從源點到終點是否已被確認是最短路徑
	int D[MVNum];//記錄從源點到終點的最短路徑長度
	int Path[MVNum];//記錄從源點到某一點是否有路徑
	int v0 = LocateVex(G, a);
	ArcNode* p = G.vertices[v0].firstarc;
	//初始化
	for (int v = 0; v< G.vexnum; v++) {
		S[v] = false;
		D[v] = Max;
		Path[v] = -1;//無弧記為-1
	}
	while (p != NULL) {
		D[p->adjvex] = p->info;
		Path[p->adjvex] = v0;//v0到v有弧
		p = p->nextarc;
	}
	S[v0] = true; D[v0] = 0;//除去源點
	//初始化結束，開始主循環，每次求得v0到某個頂點的最短路徑，將v加入S集
	for (int i = 1; i< G.vexnum; i++) {
		int min = Max;//min用來保存當前的最短路徑，初始化為極大值
		int v;//用來記錄當前終點
		for (int w = 0; w< G.vexnum; w++)
			if (!S[w] && D[w]< min) {
				v = w; min = D[w];
			}
		S[v] = true;
		//更新從v0出發到集合V-S上所有頂點的最短路徑長度
		p = G.vertices[v].firstarc;
		while (p != NULL) {
			for (int w = 0; w< G.vexnum; w++)
				if (!S[w] && (D[v] + p->info< D[w]) && w == p->adjvex) {
					D[w] = D[v] + p->info;//更新D[w]
					Path[w] = v;//更改w的前驅為v
				}
			p = p->nextarc;
		}
	}
	//算法結束，輸出從源點到各個點的最短路徑
	for (int i = 0; i< G.vexnum; i++) {
		if (i!=v0) {
			cout<< "從"<< a<< "到"<< G.vertices[i].data<< "的最短路徑長度為:";
			cout<< D[i]<< endl;
		}
	}
}
int main() {
	ALGragh G1, G2;
	cout<< "請創建帶權無向圖G1:"<< endl;
	CreateUDG(G1);
	cout<< "請創建帶權有向圖G2:"<< endl;
	CreateDG(G2);
	cout<< "深度優先遍歷圖"<< endl;
	cout<< "G1:"; DFS(G1, 'A');
	cout<< "\nG2:"; DFS(G2, 'A');
	reZero(G1); reZero(G2);
	cout<< "\n廣度優先遍歷圖"<< endl;
	cout<< "G1:"; BFS(G1, 'A');
	cout<< "\nG2:"; BFS(G2, 'A');
	cout<< "\n普利姆算法求G1的最小生成樹:"<< endl;
	MiniSpanTree_Prim(G1,'A');
	cout<< "迪杰斯特拉算法求G2的最短路徑:"<< endl;
	ShortestPath_Dijkstra(G2, 'A');
}

【功能測試】 （1）功能測試--圖的創建

圖 4.1 圖的創建測試結果

圖的創建就是先輸入圖的頂點數和邊數，然后依次輸出各頂點的信息(以空格分割)，然后根據邊的個數，依次輸入每個邊的兩個頂點和邊的權值，根據輸入的頂點值根據LocateVex函數定位頂點數組的位置，之后創建邊節點讓兩頂點指向該條邊，然后接入頂點數組的指針上，有向圖和無向圖創建的區別只在生成幾個邊節點，無向圖會生成兩個邊節點，而有向圖只生成一個，因為它有方向。

（2）功能測試--深度優先遍歷

圖 4.2 深度優先遍歷測試結果

深度優先遍歷就是用棧來實現，先進后出，在這里我用的是遞歸來實現，在圖的構造中我增加了一個標志數組(初始化值為0)用來標志訪問過的頂點，選一個頂點，然后一直遞歸深入圖，就是一條路走到黑，當頂點為空的時候再退回去繼續遞歸，訪問過的頂點，其對應的數組就設為1，直到全部的頂點全部訪問過。

（3）功能測試--廣度優先遍歷

圖 4.3 深度優先遍歷測試結果

廣度優先遍歷就是用隊列實現，先進先出，用c++標準庫里的queue隊列，將頂點保存到隊列里，先將頂點的全部鄰接頂點入隊，然后依次出隊頂點，重復循環該操作，這樣就能實現廣度優先遍歷。

（4）功能測試--Prim算法求最小生成樹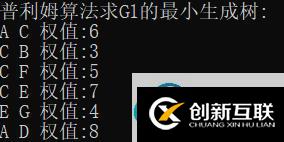

圖 4.4 Prim算法求最小生成樹測試結果

prim算法的核心就是歸并頂點，使每一次循環找最小的邊都是局部最小，然后一步步擴大它的范圍。

在本題我學習課本增加了一個存放當前頂點與其它頂點的邊的最小值closeEdge數組，然后在函數里對該數組初始化，將所有除它本身的頂點，都附上他們兩點間的權值，若兩點間沒有權值則賦予大值Max，且將初識頂點的lowcost設為0完成初始化。然后到程序的核心，首先在closeEdge數組中選擇當前頂點的最小邊作為并入最小生成樹邊的集合中，并將該邊的頂點并入最小生成樹的點中，同時將該點的lowcose置為0，說明該點已經連成，重復該步驟就能完成圖的最小生成樹。

本題的難點在于書上的例子用的是鄰接矩陣來實現，我在創建圖的過程用的是鄰接表，所以我應找出鄰接矩陣和鄰接表的不同從而對該算法的修改。

（5）功能測試--Dijkstra算法求最短路徑

圖 4.5 Dijkstra算法求最短路徑測試結果

Dijkstra算法的思想就是按路徑長度遞增的次序產生最短路徑，每寫一個頂點都是在上一個最短路徑產生的，依次修改路徑長度，從而達到最優。

在本題我從課本上學習，用了幾個數組分別來儲存路徑的信息。S數組用于記錄源點到某一個頂點是否已經是最短路徑，D數組用于記錄源點到某一個頂點的路徑長度，Path數組用于記錄某一個頂點和另一個頂點是否有弧，有弧則記錄該頂點的下標，無弧則為-1，然后根據這些定義來初始化算法。

初始化結束，開始主循環，每次求得源點到某個頂點的最短路徑，將找到的最短路徑記錄到S中。每次找到源點到某個頂點的最短路徑，都要更新S數組為false的路徑長度，重復循環完成算法。

本題的難點也是在于鄰接矩陣和鄰接表的不同從而需要對算法進行修改，比如在更新數組的時候，判斷是否是該路徑上的點需要加上該頂點是否等于p->adjvex。

你是否還在尋找穩定的海外服務器提供商？創新互聯www.cdcxhl.cn海外機房具備T級流量清洗系統配攻擊溯源，準確流量調度確保服務器高可用性，企業級服務器適合批量采購，新人活動首月15元起，快前往官網查看詳情吧

網頁標題：c++實現圖的操作(最小生成樹和最短路徑)-創新互聯
當前地址：http://www.yijiale78.com/article10/dpsido.html

成都網站建設公司_創新互聯，為您提供網站設計公司、服務器托管、外貿建站、網站維護、網站設計、App設計

廣告

聲明：本網站發布的內容（圖片、視頻和文字）以用戶投稿、用戶轉載內容為主，如果涉及侵權請盡快告知，我們將會在第一時間刪除。文章觀點不代表本網站立場，如需處理請聯系客服。電話：028-86922220；郵箱：631063699@qq.com。內容未經允許不得轉載，或轉載時需注明來源： 創新互聯