【第十三屆藍(lán)橋杯C++B組省賽編程題詳解】-創(chuàng)新互聯(lián)
【Tag:枚舉】
小明決定從下周一開(kāi)始努力刷題準(zhǔn)備藍(lán)橋杯競(jìng)賽。

他計(jì)劃周一至周五每天做a道題目,周六和周日每天做b道題目。
請(qǐng)你幫小明計(jì)算,按照計(jì)劃他將在第幾天實(shí)現(xiàn)做題數(shù)大于等于n題?
輸入格式
輸入一行包含三個(gè)整數(shù) a,b 和 n。
輸出格式
輸出一個(gè)整數(shù)代表天數(shù)。
數(shù)據(jù)范圍
對(duì)于 50% 的評(píng)測(cè)用例,
1
≤
a
,
b
,
n
≤
1
0
6
{1≤a,b,n≤10^6}
1≤a,b,n≤106,
對(duì)于 100% 的評(píng)測(cè)用例,
1
≤
a
,
b
,
n
≤
1
0
18
{1≤a,b,n≤10^{18}}
1≤a,b,n≤1018。
輸入樣例:
10 20 99輸出樣例:
8我們可以先統(tǒng)計(jì)出每周刷題數(shù)目s,然后求出有多少個(gè)整周的天數(shù)res。
接著求出我們還要做多少題目n,最后把余數(shù)加起來(lái)即可。
注意:數(shù)據(jù)范圍一定要考慮!!!
實(shí)現(xiàn)#include#include#include
using namespace std;
typedef long long LL;
LL a, b, n;
int main()
{
scanf("%lld%lld%lld", &a, &b, & n);
LL s = 5 * a + 2 * b; //每周的刷題數(shù)
LL res = n / s * 7; //整周的天數(shù)
n %= s; //剩余的題目數(shù)量
LL d[] = {a, a, a, a, a, b, b};
for (int i = 0; n >0; i ++)
{
n -= d[i];
res ++;
}
printf("%lld\n", res);
return 0;
}
【Tag:模擬】
愛(ài)麗絲要完成一項(xiàng)修剪灌木的工作。有N棵灌木整齊的從左到右排成一排。
愛(ài)麗絲在每天傍晚會(huì)修剪一棵灌木,讓灌木的高度變?yōu)?code>0厘米。
愛(ài)麗絲修剪灌木的順序是從最左側(cè)的灌木開(kāi)始,每天向右修剪一棵灌木。
當(dāng)修剪了最右側(cè)的灌木后,她會(huì)調(diào)轉(zhuǎn)方向,下一天開(kāi)始向左修剪灌木。
直到修剪了最左的灌木后再次調(diào)轉(zhuǎn)方向。然后如此循環(huán)往復(fù)。
灌木每天從早上到傍晚會(huì)長(zhǎng)高1厘米,而其余時(shí)間不會(huì)長(zhǎng)高。
在第一天的早晨,所有灌木的高度都是0厘米。愛(ài)麗絲想知道每棵灌木最高長(zhǎng)到多高。
輸入格式
一個(gè)正整數(shù) N,含義如題面所述。
輸出格式
輸出 N 行,每行一個(gè)整數(shù),第 i 行表示從左到右第 i 棵樹(shù)最高能長(zhǎng)到多高。
數(shù)據(jù)范圍 輸入樣例: 輸出樣例: 我們可以簡(jiǎn)單的模擬出每棵樹(shù)的高度變化。 每棵樹(shù)的高度: 注意:加粗的數(shù)字為我們要修剪的樹(shù)木。 我們可以看出是一個(gè)循環(huán)的序列,總結(jié)出每個(gè)樹(shù)可以長(zhǎng)到的大高度為 【Tag:數(shù)學(xué)】 X 進(jìn)制是一種很神奇的進(jìn)制,因?yàn)槠涿恳粩?shù)位的進(jìn)制并不固定! 例如說(shuō)某種 X 進(jìn)制數(shù),最低數(shù)位為二進(jìn)制,第二數(shù)位為十進(jìn)制,第三數(shù)位為八進(jìn)制,則 X 進(jìn)制數(shù) 現(xiàn)在有兩個(gè) X 進(jìn)制表示的整數(shù) 請(qǐng)你算出 請(qǐng)注意,你需要保證 輸入格式 第二行一個(gè)正整數(shù)
M
a
{M_a}
Ma?,表示 X 進(jìn)制數(shù) A 的位數(shù)。 第三行
M
a
{M_a}
Ma? 個(gè)用空格分開(kāi)的整數(shù),表示 X 進(jìn)制數(shù) A 按從高位到低位順序各個(gè)數(shù)位上的數(shù)字在十進(jìn)制下的表示。 第四行一個(gè)正整數(shù)
M
b
{M_b}
Mb?,表示 X 進(jìn)制數(shù) B 的位數(shù)。 第五行
M
b
{M_b}
Mb? 個(gè)用空格分開(kāi)的整數(shù),表示 X 進(jìn)制數(shù) B 按從高位到低位順序各個(gè)數(shù)位上的數(shù)字在十進(jìn)制下的表示。 請(qǐng)注意,輸入中的所有數(shù)字都是十進(jìn)制的。 輸出格式 數(shù)據(jù)范圍 輸入樣例: 輸出樣例: 樣例解釋 此時(shí) A 在十進(jìn)制下是 108,B 在十進(jìn)制下是 14,差值是 94。 我們平常所見(jiàn)到的數(shù)字,他的每一位數(shù)的進(jìn)制都是相同的,每位數(shù)字的權(quán)重是
X
n
{X^n}
Xn(n為該位數(shù)字后面的位數(shù)),比如二進(jìn)制1000中首位的1的權(quán)重是
2
3
{2^3}
23=8。 對(duì)于題目中的樣例,某種 使用記次數(shù)的方式理解進(jìn)制 最低位為二進(jìn)制,“逢二進(jìn)一”,最低為為1; 第二位為十進(jìn)制,“逢十進(jìn)一”,計(jì)數(shù)法進(jìn)位會(huì)經(jīng)過(guò)0,1,10,11,20,所以我們數(shù)
2
×
2
{2 × 2}
2×2次便會(huì)得到2。 第三位為八進(jìn)制,“逢八進(jìn)一”,計(jì)數(shù)法進(jìn)位會(huì)經(jīng)過(guò)0,1,10,11,20,21,30,31,40,41,50,51,60,61,70,71,80,81,90,91,100,…310,311,320,321,結(jié)束計(jì)數(shù),我們會(huì)經(jīng)過(guò)
3
×
10
×
2
{3 × 10 × 2 }
3×10×2次得到3。 由此我們可以看出在本題各位數(shù)字進(jìn)制不同情況下,該位數(shù)字的權(quán)重其實(shí)是后面各位數(shù)字的進(jìn)制的乘積。 進(jìn)制類(lèi)似于蓋大樓,要想高數(shù)位上有數(shù)字,就必須時(shí)底數(shù)位上有數(shù)字,并且滿足條件。 【Tag:前綴和, 雙指針】 給定一個(gè) N×M 的矩陣 A,請(qǐng)你統(tǒng)計(jì)有多少個(gè)子矩陣 (最小 1×1,大 N×M) 滿足子矩陣中所有數(shù)的和不超過(guò)給定的整數(shù) K? 輸入格式 之后 N 行每行包含 M 個(gè)整數(shù),代表矩陣 A。 輸出格式 數(shù)據(jù)范圍 輸入樣例: 輸出樣例: 樣例解釋 我們要求出滿足條件(子矩陣的和不超過(guò)K的矩陣數(shù)量),先使用前綴個(gè)處理出數(shù)組和。然后采用暴力去求解問(wèn)題,發(fā)現(xiàn)每一維都有500的范圍,所以我們的時(shí)間復(fù)雜度會(huì)在
50
0
4
{500^4}
5004左右,會(huì)面臨超時(shí)的風(fēng)險(xiǎn)。 我們使用雙指針進(jìn)行優(yōu)化,我們可以先確定出上下邊界,然后動(dòng)態(tài)去求解左右邊界。 優(yōu)化方法為: 優(yōu)化之后時(shí)間復(fù)雜度為
O
(
N
3
)
{O(N^3)}
O(N3)。 【Tag:DP】 同時(shí),小明有一塊面積大小為 2×N 的畫(huà)布,畫(huà)布由 2×N 個(gè) 1×1 區(qū)域構(gòu)成。 小明需要用以上兩種積木將畫(huà)布拼滿,他想知道總共有多少種不同的方式? 積木可以任意旋轉(zhuǎn),且畫(huà)布的方向固定。 輸入格式 輸出格式 由于答案可能很大,所以輸出其對(duì) 1000000007 取模后的值。 數(shù)據(jù)范圍 輸入樣例: 狀態(tài)壓縮DP類(lèi)型。 狀態(tài)表示: 狀態(tài)計(jì)算:因?yàn)榇祟}的轉(zhuǎn)換數(shù)量很少,只有16種可能,所以我們進(jìn)行枚舉即可。 樸素版:時(shí)間高,空間高 使用滾動(dòng)數(shù)組優(yōu)化:空間低,時(shí)間高 優(yōu)化常數(shù):空間低,時(shí)間低 【Tag: 哈希表,搜索】 在一個(gè)二維平面上放置著 n 個(gè)炸雷,第 i 個(gè)炸雷
(
x
i
,
y
i
,
r
i
)
{(x_i,y_i,r_i)}
(xi?,yi?,ri?) 表示在坐標(biāo)
(
x
i
,
y
i
)
{(x_i,y_i)}
(xi?,yi?) 處存在一個(gè)炸雷,它的爆炸范圍是以半徑為
r
i
{r_i}
ri? 的一個(gè)圓。 為了順利通過(guò)這片土地,需要玩家進(jìn)行排雷。 玩家可以發(fā)射 m 個(gè)排雷火箭,小明已經(jīng)規(guī)劃好了每個(gè)排雷火箭的發(fā)射方向,第 j 個(gè)排雷火箭
(
x
j
,
y
j
,
r
j
)
{(x_j,y_j,r_j)}
(xj?,yj?,rj?) 表示這個(gè)排雷火箭將會(huì)在
(
x
j
,
y
j
)
{(x_j,y_j)}
(xj?,yj?) 處爆炸,它的爆炸范圍是以半徑為
r
j
{r_j}
rj? 的一個(gè)圓,在其爆炸范圍內(nèi)的炸雷會(huì)被引爆。 同時(shí),當(dāng)炸雷被引爆時(shí),在其爆炸范圍內(nèi)的炸雷也會(huì)被引爆。 現(xiàn)在小明想知道他這次共引爆了幾顆炸雷? 你可以把炸雷和排雷火箭都視為平面上的一個(gè)點(diǎn)。 一個(gè)點(diǎn)處可以存在多個(gè)炸雷和排雷火箭。 當(dāng)炸雷位于爆炸范圍的邊界上時(shí)也會(huì)被引爆。 輸入格式 接下來(lái)的 n 行,每行三個(gè)整數(shù)
x
i
,
y
i
,
r
i
{x_i,y_i,r_i}
xi?,yi?,ri?,表示一個(gè)炸雷的信息。 再接下來(lái)的 m 行,每行三個(gè)整數(shù)
x
j
,
y
j
,
r
j
{x_j,y_j,r_j}
xj?,yj?,rj?,表示一個(gè)排雷火箭的信息。 輸出格式 數(shù)據(jù)范圍 對(duì)于 100% 的評(píng)測(cè)用例:
0
≤
x
,
y
≤
1
0
9
,
0
≤
n
,
m
≤
5
×
1
0
4
,
1
≤
r
≤
10
{0≤x,y≤10^9,0≤n,m≤5×10^4,1≤r≤10}
0≤x,y≤109,0≤n,m≤5×104,1≤r≤10。 示例圖如下,排雷火箭 1 覆蓋了炸雷 1,所以炸雷 1 被排除;炸雷 1 又覆蓋了炸雷 2,所以炸雷 2 也被排除。 手寫(xiě)哈希表+搜索 【Tag:DP】 一天,他提著酒壺,從家里出來(lái),酒壺中有酒 2 斗。 他邊走邊唱: 無(wú)事街上走,提壺去打酒。 逢店加一倍,遇花喝一斗。 這一路上,他一共遇到店 N 次,遇到花 M 次。 已知最后一次遇到的是花,他正好把酒喝光了。 請(qǐng)你計(jì)算李白這一路遇到店和花的順序,有多少種不同的可能? 注意:壺里沒(méi)酒 (0 斗) 時(shí)遇店是合法的,加倍后還是沒(méi)酒;但是沒(méi)酒時(shí)遇花是不合法的。 輸入格式 輸出格式 數(shù)據(jù)范圍 輸入樣例: 輸出樣例: 樣例解釋 動(dòng)態(tài)規(guī)劃題,使用閆氏DP分析法求解。 狀態(tài)表示: 狀態(tài)屬性:數(shù)量。 狀態(tài)計(jì)算: 分為兩種: 這天,小明在砍竹子,他面前有n棵竹子排成一排,一開(kāi)始第i棵竹子的高度為
h
i
{h_i}
hi?。 他覺(jué)得一棵一棵砍太慢了,決定使用魔法來(lái)砍竹子。 魔法可以對(duì)連續(xù)的一段相同高度的竹子使用,假設(shè)這一段竹子的高度為 H,那么使用一次魔法可以把這一段竹子的高度都變?yōu)?
?
?
H
2
?
+
1
?
?\sqrt{?\frac {H}{2}?+1}?
??2H??+1
?? ,其中 ?x? 表示對(duì) x 向下取整。 小明想知道他最少使用多少次魔法可以讓所有的竹子的高度都變?yōu)?1。 輸入格式 第二行共 n 個(gè)空格分開(kāi)的正整數(shù) hi,表示每棵竹子的高度。 輸出格式 數(shù)據(jù)范圍 輸入樣例: 輸出樣例: 樣例解釋 我們現(xiàn)預(yù)處理需要進(jìn)行的大高度。 輸出結(jié)果為 可以看出每個(gè)數(shù)大的操作次數(shù)為6次,題目的數(shù)據(jù)量為
1
≤
n
≤
2
×
1
0
5
{1≤n≤2×10^5}
1≤n≤2×105,所以我們可以使用暴力法去求解。 我們先對(duì)每個(gè)數(shù)進(jìn)行預(yù)處理,將預(yù)處理后的數(shù)據(jù)存儲(chǔ)起來(lái),題目中說(shuō)我們可以對(duì)連續(xù)的一段相同高度的竹子進(jìn)行操作,所以我們?cè)谂袛噙B續(xù)的一段竹子的高度是否相等即可。 主要想收集一下,閱讀者對(duì)我書(shū)寫(xiě)文章、題解時(shí)的建議或者看法。 歡迎各位讀者留言,評(píng)論。 你是否還在尋找穩(wěn)定的海外服務(wù)器提供商?創(chuàng)新互聯(lián)www.cdcxhl.cn海外機(jī)房具備T級(jí)流量清洗系統(tǒng)配攻擊溯源,準(zhǔn)確流量調(diào)度確保服務(wù)器高可用性,企業(yè)級(jí)服務(wù)器適合批量采購(gòu),新人活動(dòng)首月15元起,快前往官網(wǎng)查看詳情吧
新聞名稱(chēng):【第十三屆藍(lán)橋杯C++B組省賽編程題詳解】-創(chuàng)新互聯(lián)
成都網(wǎng)站建設(shè)公司_創(chuàng)新互聯(lián),為您提供網(wǎng)站排名、微信公眾號(hào)、網(wǎng)站設(shè)計(jì)、手機(jī)網(wǎng)站建設(shè)、響應(yīng)式網(wǎng)站、品牌網(wǎng)站建設(shè)
聲明:本網(wǎng)站發(fā)布的內(nèi)容(圖片、視頻和文字)以用戶投稿、用戶轉(zhuǎn)載內(nèi)容為主,如果涉及侵權(quán)請(qǐng)盡快告知,我們將會(huì)在第一時(shí)間刪除。文章觀點(diǎn)不代表本網(wǎng)站立場(chǎng),如需處理請(qǐng)聯(lián)系客服。電話:028-86922220;郵箱:631063699@qq.com。內(nèi)容未經(jīng)允許不得轉(zhuǎn)載,或轉(zhuǎn)載時(shí)需注明來(lái)源:
創(chuàng)新互聯(lián)
對(duì)于 30% 的數(shù)據(jù),N≤10,
對(duì)于 100% 的數(shù)據(jù),13
思路分析4
2
4天數(shù) 第一棵樹(shù) 第二棵樹(shù) 第三棵樹(shù) 第四棵樹(shù) 第五棵樹(shù) ① 1 1 1 1 1 ② 1 2 2 2 2 ③ 2 1 3 3 3 ④ 3 2 1 4 4 ⑤ 4 3 2 1 5 ⑥ 5 4 3 2 1 ⑦ 6 5 4 1 2 ⑧ 7 6 1 2 3 ⑨ 8 1 2 3 4 ⑩ 1 2 3 4 5 … … … … … … max(i - 1, n - i ) * 2
第三題: X 進(jìn)制減法
題目描述#include
進(jìn)制規(guī)定了數(shù)字在數(shù)位上逢幾進(jìn)一。321轉(zhuǎn)換為十進(jìn)制數(shù)為65。A和B,但是其具體每一數(shù)位的進(jìn)制還不確定,只知道A和B是同一進(jìn)制規(guī)則,且每一數(shù)位最高為N進(jìn)制,最低為二進(jìn)制。A?B的結(jié)果最小可能是多少。A和B在 X 進(jìn)制下都是合法的,即每一數(shù)位上的數(shù)字要小于其進(jìn)制。
第一行一個(gè)正整數(shù) N,含義如題面所述。
輸出一行一個(gè)整數(shù),表示 X 進(jìn)制數(shù) A?B 的結(jié)果的最小可能值轉(zhuǎn)換為十進(jìn)制后再模 1000000007 的結(jié)果。
對(duì)于 30% 的數(shù)據(jù),
N
≤
10
;
M
a
,
M
b
≤
8
{N≤10;M_a,M_b≤8}
N≤10;Ma?,Mb?≤8,
對(duì)于 100% 的數(shù)據(jù),
2
≤
N
≤
1000
;
1
≤
M
a
,
M
b
≤
100000
;
A
≥
B
{2≤N≤1000;1≤M_a,M_b≤100000;A≥B}
2≤N≤1000;1≤Ma?,Mb?≤100000;A≥B。11
3
10 4 0
3
1 2 094
當(dāng)進(jìn)制為:最低位 2 進(jìn)制,第二數(shù)位 5 進(jìn)制,第三數(shù)位 11 進(jìn)制時(shí),減法得到的差最小。X進(jìn)制數(shù),最低數(shù)位為二進(jìn)制,第二數(shù)位為十進(jìn)制,第三數(shù)位為八進(jìn)制,則X進(jìn)制數(shù)321轉(zhuǎn)換為十進(jìn)制數(shù)為65。
對(duì)于任意一個(gè)P我們可以將其分為兩部分:包含P與不包含P。
所以我們每次取最小值時(shí),必須滿足每一位進(jìn)制P取最小值即可。
最小值為{ai+1,bi+1,2},這三個(gè)數(shù)取最小值。(此處的+1,與2防止出現(xiàn)1進(jìn)制)。
使用秦九韶算法進(jìn)行進(jìn)制計(jì)算的優(yōu)化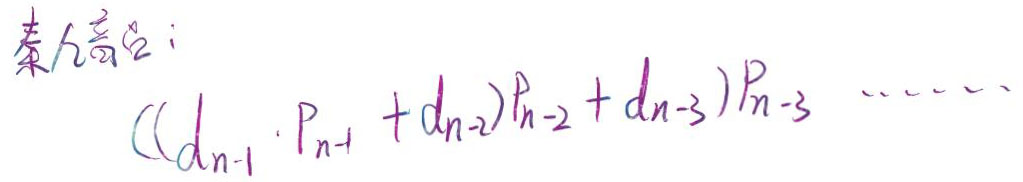
第四題:統(tǒng)計(jì)子數(shù)組#include
第一行包含三個(gè)整數(shù) N,M 和 K。
一個(gè)整數(shù)代表答案。
對(duì)于 30% 的數(shù)據(jù),N,M≤20,
對(duì)于 70% 的數(shù)據(jù),N,M≤100,
對(duì)于 100% 的數(shù)據(jù),1≤N, M≤500;0≤Aij≤1000;1≤K≤2.5×108。3 4 10
1 2 3 4
5 6 7 8
9 10 11 1219
滿足條件的子矩陣一共有 19,包含:
思路描述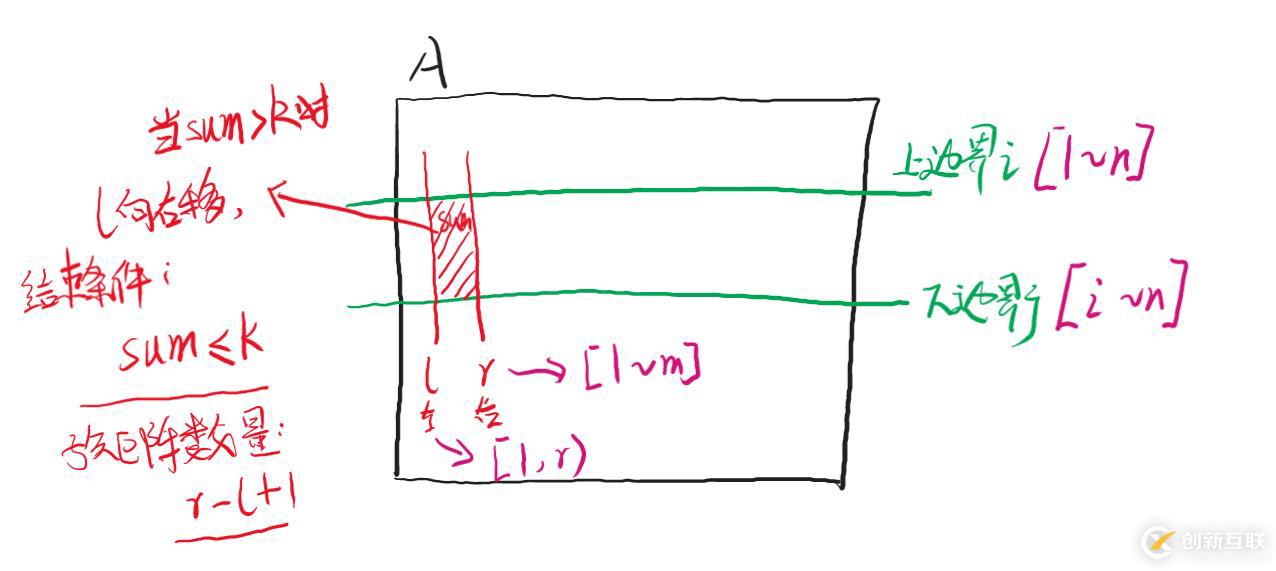
第五題:積木畫(huà)#include
小明最近迷上了積木畫(huà),有這么兩種類(lèi)型的積木,分別為 I 型(大小為 2 個(gè)單位面積)和 L 型(大小為 3 個(gè)單位面積):
輸入一個(gè)整數(shù) N,表示畫(huà)布大小。
輸出一個(gè)整數(shù)表示答案。
1
≤
N
≤
1
0
7
{1≤N≤10^7}
1≤N≤107。
3
輸出樣例:
5
樣例解釋
五種情況如下圖所示,顏色只是為了標(biāo)識(shí)不同的積木: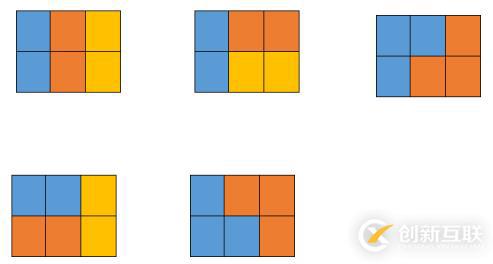
f[i][j]表示前i - 1個(gè)位置已經(jīng)確定,并且第i個(gè)狀態(tài)為j的方案。#include#include
第六題:掃雷#include
小明最近迷上了一款名為《掃雷》的游戲。其中有一個(gè)關(guān)卡的任務(wù)如下:
輸入的第一行包含兩個(gè)整數(shù) n、m。
輸出一個(gè)整數(shù)表示答案。
對(duì)于 40% 的評(píng)測(cè)用例:
0
≤
x
,
y
≤
1
0
9
,
0
≤
n
,
m
≤
1
0
3
,
1
≤
r
≤
10
{0≤x,y≤10^9,0≤n,m≤10^3,1≤r≤10}
0≤x,y≤109,0≤n,m≤103,1≤r≤10,
樣例解釋輸入樣例:
2 1
2 2 4
4 4 2
0 0 5
輸出樣例:
2
第七題:李白打酒加強(qiáng)版#include
話說(shuō)大詩(shī)人李白,一生好飲。幸好他從不開(kāi)車(chē)。
第一行包含兩個(gè)整數(shù) N 和 M。
輸出一個(gè)整數(shù)表示答案。由于答案可能很大,輸出模 1000000007 的結(jié)果。
對(duì)于 40% 的評(píng)測(cè)用例:1≤N,M≤10。
對(duì)于 100% 的評(píng)測(cè)用例:1≤N,M≤100。5 1014
如果我們用 0 代表遇到花,1 代表遇到店,14 種順序如下:
思路描述010101101000000
010110010010000
011000110010000
100010110010000
011001000110000
100011000110000
100100010110000
010110100000100
011001001000100
100011001000100
100100011000100
011010000010100
100100100010100
101000001010100f(i,j,k)分別表示為經(jīng)過(guò)第i朵店,第j個(gè)花時(shí),酒壺中酒的數(shù)量為k。
實(shí)現(xiàn)
第八題:砍竹子#include
第一行為一個(gè)正整數(shù) n,表示竹子的棵數(shù)。
一個(gè)整數(shù)表示答案。
對(duì)于 20% 的數(shù)據(jù),保證
1
≤
n
≤
1000
,
1
≤
h
i
≤
1
0
6
{1≤n≤1000,1≤h_i≤10^6}
1≤n≤1000,1≤hi?≤106 。
對(duì)于 100% 的數(shù)據(jù),保證
1
≤
n
≤
2
×
1
0
5
,
1
≤
h
i
≤
1
0
18
{1≤n≤2×10^5,1≤h_i≤10^{18}}
1≤n≤2×105,1≤hi?≤1018。6
2 1 4 2 6 75
其中一種方案:
思路描述2 1 4 2 6 7
→ 2 1 4 2 6 2
→ 2 1 4 2 2 2
→ 2 1 1 2 2 2
→ 1 1 1 2 2 2
→ 1 1 1 1 1 1
共需要 5 步完成。#include707106781
18803
96
7
2
1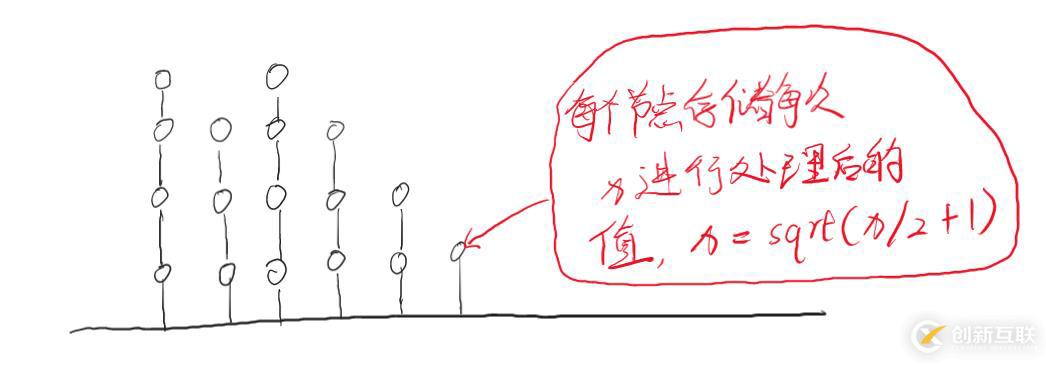
調(diào)研#include
URL地址:http://www.yijiale78.com/article22/psgjc.html
猜你還喜歡下面的內(nèi)容

- 中小型企業(yè)出具網(wǎng)站策劃書(shū) 包括哪些內(nèi)容 2016-04-28
- 網(wǎng)站策劃為網(wǎng)站推廣提供有利保證 2021-01-08
- 網(wǎng)站策劃設(shè)計(jì) 2016-06-03
- 成都網(wǎng)站建設(shè)-高端定制網(wǎng)站策劃需要要怎么做 2016-10-09
- 為什么說(shuō)網(wǎng)站策劃比建站技術(shù)更重要? 2022-08-10
- 網(wǎng)站建設(shè):論營(yíng)銷(xiāo)網(wǎng)站策劃的重要性,學(xué)到了! 2022-08-17
- 分析做網(wǎng)站策劃對(duì)營(yíng)銷(xiāo)型網(wǎng)站真的重要嗎? 2022-12-17
- 成都補(bǔ)習(xí)學(xué)校淺析網(wǎng)站策劃的重要性與意義是什么? 2016-02-16
- 企業(yè)網(wǎng)站建設(shè)方案策劃書(shū)如何寫(xiě)?企業(yè)網(wǎng)站策劃書(shū) 2022-08-26
- 【網(wǎng)絡(luò)推廣】結(jié)合搜索營(yíng)銷(xiāo)、手機(jī)推廣、網(wǎng)站策劃制定有效的網(wǎng)絡(luò)推廣策略 2022-05-02
- 營(yíng)銷(xiāo)型網(wǎng)站策劃及網(wǎng)站建設(shè)的思路 2014-05-26
- 物流公司企業(yè)網(wǎng)站策劃書(shū) 2022-06-03