Java數據結構與算法實例講解
這篇文章主要講解了“Java數據結構與算法實例講解”,文中的講解內容簡單清晰,易于學習與理解,下面請大家跟著小編的思路慢慢深入,一起來研究和學習“Java數據結構與算法實例講解”吧!
創新互聯專業為企業提供宜黃網站建設、宜黃做網站、宜黃網站設計、宜黃網站制作等企業網站建設、網頁設計與制作、宜黃企業網站模板建站服務,十多年宜黃做網站經驗,不只是建網站,更提供有價值的思路和整體網絡服務。
為什么需要樹這種結構
1.數組存儲方式分析:
優點:通過下標方式訪問元素,速度快。對于有序數組,還可以使用二分查找提高檢索速度。
缺點:如果檢索某個具體的值,或者插入值(按一定的順序)會整體移動,效率較低。
2.鏈式存儲方式分析:
優點:在一定程度上對數組存儲方式優化(比如:插入一個數值節點,只需要將插入節點,鏈接到鏈表中即可,刪除效率很高)。
缺點:在進行檢索時,效率仍然很低,需要從頭結點開始遍歷。
3.樹存儲方式分析:能提高數據存儲,讀取的效率,比如利用二叉排序樹(Binary sort tree),即可以保證數據的檢索速度,同時也可以保證數據的插入、刪除、修改的速度。假設一組[7,3,10,1,5,9,12]以樹的方式存儲,分析如下圖:
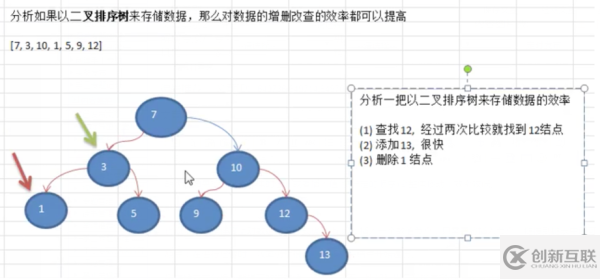
二叉樹的前序遍歷、中序遍歷、后序遍歷
前序遍歷:輸出父節點、輸出左邊節點、輸出右邊節點;
中序遍歷:輸出左邊節點、輸出父節點、輸出右邊節點;
后序遍歷:輸出左邊節點、輸出右邊節點、輸出父節點;
需求案例
完成一個如下二叉樹節點存儲、前序遍歷搜索、中序遍歷搜索、后序遍歷搜索和刪除節點功能。
對于刪除節點要求如下:
鴻蒙官方戰略合作共建——HarmonyOS技術社區
如果刪除的節點是葉子節點,則刪除該節點。
如果刪除的節點是非葉子節點,則刪除該樹。
測試,刪除5號葉子節點和3號子樹。
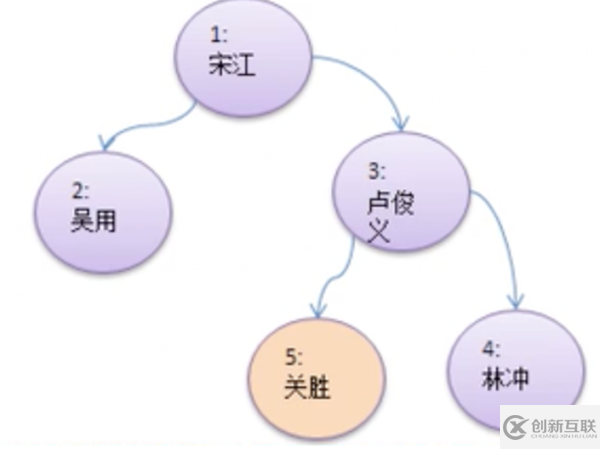
代碼案例
package com.xie.tree; public class BinaryTreeDemo { public static void main(String[] args) { BinaryTree binaryTree = new BinaryTree(); HeroNode root = new HeroNode(1, "宋江"); HeroNode node2 = new HeroNode(2, "吳用"); HeroNode node3 = new HeroNode(3, "盧俊義"); HeroNode node4 = new HeroNode(4, "林沖"); HeroNode node5 = new HeroNode(5, "關勝"); //先手動創建該二叉樹,后面用遞歸方式 root.setLeft(node2); root.setRight(node3); node3.setRight(node4); node3.setLeft(node5); binaryTree.setRoot(root); //前序遍歷 System.out.println("前序遍歷"); binaryTree.preOrder(); //中序遍歷 System.out.println("中序遍歷"); binaryTree.infixOrder(); //后續遍歷 System.out.println("后續遍歷"); binaryTree.postOrder(); //前序遍歷查找 System.out.println("前序遍歷查找~~"); HeroNode resultNode = binaryTree.preOrderSearch(5); if (resultNode != null) { System.out.printf("找到了,信息為no=%d,name=%s\n", resultNode.getNo(), resultNode.getName()); System.out.println("遍歷次數:" + HeroNode.preCount); } else { System.out.println("沒有找到"); } //中序遍歷查找 System.out.println("中序遍歷查找~~"); HeroNode resultNode1 = binaryTree.infixOrderSearch(5); if (resultNode1 != null) { System.out.printf("找到了,信息為no=%d,name=%s\n", resultNode1.getNo(), resultNode1.getName()); System.out.println("遍歷次數:" + HeroNode.infoxCount); } else { System.out.println("沒有找到"); } //后序遍歷查找 System.out.println("后序遍歷查找~~"); HeroNode resultNode2 = binaryTree.postOrderSearch(5); if (resultNode2 != null) { System.out.printf("找到了,信息為no=%d,name=%s\n", resultNode2.getNo(), resultNode2.getName()); System.out.println("遍歷次數:" + HeroNode.postCount); } else { System.out.println("沒有找到"); } System.out.println("刪除3號節點"); binaryTree.delNo(3); System.out.println("刪除后的節點"); binaryTree.preOrder(); /** * 前序遍歷 * HeroNode{no=1, name=宋江} * HeroNode{no=2, name=吳用} * HeroNode{no=3, name=盧俊義} * HeroNode{no=5, name=關勝} * HeroNode{no=4, name=林沖} * 中序遍歷 * HeroNode{no=2, name=吳用} * HeroNode{no=1, name=宋江} * HeroNode{no=5, name=關勝} * HeroNode{no=3, name=盧俊義} * HeroNode{no=4, name=林沖} * 后續遍歷 * HeroNode{no=2, name=吳用} * HeroNode{no=5, name=關勝} * HeroNode{no=4, name=林沖} * HeroNode{no=3, name=盧俊義} * HeroNode{no=1, name=宋江} * 前序遍歷查找~~ * 找到了,信息為no=5,name=關勝 * 遍歷次數:4 * 中序遍歷查找~~ * 找到了,信息為no=5,name=關勝 * 遍歷次數:3 * 后序遍歷查找~~ * 找到了,信息為no=5,name=關勝 * 遍歷次數:2 * 刪除3號節點 * 刪除后的節點 * HeroNode{no=1, name=宋江} * HeroNode{no=2, name=吳用} */ } } class BinaryTree { private HeroNode root; public void setRoot(HeroNode root) { this.root = root; } //前序遍歷 public void preOrder() { if (this.root != null) { this.root.preOrder(); } } //中序遍歷 public void infixOrder() { if (this.root != null) { this.root.infixOrder(); } } //刪除節點 public void delNo(int no) { if (this.root != null) { if (this.root.getNo() == no) { this.root = null; } else { this.root.delNo(no); } } return; } //后序遍歷 public void postOrder() { if (this.root != null) { this.root.postOrder(); } } //前序遍歷查找 public HeroNode preOrderSearch(int no) { if (root != null) { return root.preOrderSearch(no); } else { return null; } } //中序遍歷查找 public HeroNode infixOrderSearch(int no) { if (root != null) { return root.infixOrderSearch(no); } else { return null; } } //后序遍歷查找 public HeroNode postOrderSearch(int no) { if (root != null) { return root.postOrderSearch(no); } else { return null; } } } class HeroNode { static int preCount = 0; static int infoxCount = 0; static int postCount = 0; private int no; private String name; private HeroNode left; private HeroNode right; public HeroNode(int no, String name) { this.no = no; this.name = name; } public int getNo() { return no; } public void setNo(int no) { this.no = no; } public String getName() { return name; } public void setName(String name) { this.name = name; } public HeroNode getLeft() { return left; } public void setLeft(HeroNode left) { this.left = left; } public HeroNode getRight() { return right; } public void setRight(HeroNode right) { this.right = right; } @Override public String toString() { return "HeroNode{" + "no=" + no + ", name=" + name + '}'; } //前序遍歷 public void preOrder() { System.out.println(this); //遞歸向左子樹前序遍歷 if (this.left != null) { this.left.preOrder(); } //遞歸向右子樹前序遍歷 if (this.right != null) { this.right.preOrder(); } } //中序遍歷 public void infixOrder() { //遞歸向左子樹中序遍歷 if (this.left != null) { this.left.infixOrder(); } System.out.println(this); //遞歸向右子樹中序遍歷 if (this.right != null) { this.right.infixOrder(); } } //后序遍歷 public void postOrder() { //遞歸向左子樹后序遍歷 if (this.left != null) { this.left.postOrder(); } //遞歸向右子樹后序遍歷 if (this.right != null) { this.right.postOrder(); } System.out.println(this); } //遞歸刪除節點 //1.如果刪除的節點是葉子節點,則刪除該節點。 //2.如果刪除的節點是非葉子節點,則刪除該樹。 public void delNo(int no) { /** * 1.因為我們的二叉樹是單向的,所以我們是判斷當前節點的子節點是否是需要刪除的節點,而不能去判斷當前節點是否是需要刪除的節點。 * 2.如果當前節點的左子節點不為空,并且左子節點就是需要刪除的節點,就將this.left = null;并且返回(結束遞歸)。 * 3.如果當前節點的右子節點不為空,并且右子節點就是需要刪除的節點,將將this.right = null;并且返回(結束遞歸)。 * 4.如果第2步和第3步沒有刪除節點,那么就要向左子樹進行遞歸刪除。 * 5.如果第4步也沒有刪除節點,則應當向右子樹進行遞歸刪除。 */ if (this.left != null && this.left.no == no) { this.left = null; return; } if (this.right != null && this.right.no == no) { this.right = null; return; } if (this.left != null) { this.left.delNo(no); } if (this.right != null) { this.right.delNo(no); } } //前序遍歷查找 public HeroNode preOrderSearch(int no) { HeroNode res = null; preCount++;//這里必須放在this.no == no 判斷之前,才進行實際的比較 //若果找到,就返回 if (this.no == no) { return this; } //沒有找到,向左子樹遞歸進行前序查找 if (this.left != null) { res = this.left.preOrderSearch(no); } //如果res != null 就直接返回 if (res != null) { return res; } //如果左子樹沒有找打,向右子樹進行前序查找 if (this.right != null) { res = this.right.preOrderSearch(no); } //如果找到就返回 if (res != null) { return res; } return res; } //中序遍歷查找 public HeroNode infixOrderSearch(int no) { HeroNode res = null; if (this.left != null) { res = this.left.infixOrderSearch(no); } if (res != null) { return res; } infoxCount++;//這里必須放在this.no == no 判斷之前,才進行實際的比較 if (this.no == no) { return this; } if (this.right != null) { res = this.right.infixOrderSearch(no); } if (res != null) { return res; } return res; } //后序遍歷查找 public HeroNode postOrderSearch(int no) { HeroNode res = null; if (this.left != null) { res = this.left.postOrderSearch(no); } if (res != null) { return res; } if (this.right != null) { res = this.right.postOrderSearch(no); } if (res != null) { return res; } postCount++;//這里必須放在this.no == no 判斷之前,才進行實際的比較 if (this.no == no) { return this; } return res; } }感謝各位的閱讀,以上就是“Java數據結構與算法實例講解”的內容了,經過本文的學習后,相信大家對Java數據結構與算法實例講解這一問題有了更深刻的體會,具體使用情況還需要大家實踐驗證。這里是創新互聯,小編將為大家推送更多相關知識點的文章,歡迎關注!
文章題目:Java數據結構與算法實例講解
文章源于:http://www.yijiale78.com/article30/gihdpo.html
成都網站建設公司_創新互聯,為您提供移動網站建設、做網站、定制開發、網站營銷、微信公眾號、網站排名
聲明:本網站發布的內容(圖片、視頻和文字)以用戶投稿、用戶轉載內容為主,如果涉及侵權請盡快告知,我們將會在第一時間刪除。文章觀點不代表本網站立場,如需處理請聯系客服。電話:028-86922220;郵箱:631063699@qq.com。內容未經允許不得轉載,或轉載時需注明來源: 創新互聯

- 邏輯思維:軟件開發行業的發展趨勢 2016-08-02
- 成都物流軟件開發該注意哪些問題? 2022-06-08
- 小白如何零基礎學習APP軟件開發? 2021-06-11
- 智慧停車APP軟件開發包括哪些功能呢? 2023-02-24
- 自學編程面試技巧,軟件開發? 2022-03-30
- APP軟件開發如何滿足用戶的需求 2016-08-13
- 成都現代化家居APP軟件開發,成都現代化家居APP軟件制作 2022-06-24
- 同樣軟件開發工程師,為何他待遇那么好? 2021-03-19
- 人事檔案信息管理系統軟件開發要注意哪些問題呢 2016-11-12
- 手機app軟件開發對企業和創業者有什么意義? 2016-08-05
- 來自軟件開發公司的網站設計分享 2022-04-21
- IT 人眼里最吃香的技術:軟件開發 JavaScript;數據專業 R等 2021-02-23