本篇文章給大家分享的是有關關于JavaScript二叉樹的詳細介紹，小編覺得挺實用的，因此分享給大家學習，希望大家閱讀完這篇文章后可以有所收獲，話不多說，跟著小編一起來看看吧。

為馬關等地區用戶提供了全套網頁設計制作服務，及馬關網站建設行業解決方案。主營業務為網站建設、網站設計、馬關網站設計，以傳統方式定制建設網站，并提供域名空間備案等一條龍服務，秉承以專業、用心的態度為用戶提供真誠的服務。我們深信只要達到每一位用戶的要求，就會得到認可，從而選擇與我們長期合作。這樣，我們也可以走得更遠！

可能有一部分人沒有讀過我上一篇寫的二叉堆，所以這里把二叉樹的基本概念復制過來了，如果讀過的人可以忽略前面針對二叉樹基本概念的介紹，另外如果對鏈表數據結構不清楚的最好先看一下本人之前寫的js數據結構-鏈表

二叉樹

二叉樹(Binary Tree)是一種樹形結構，它的特點是每個節點最多只有兩個分支節點，一棵二叉樹通常由根節點，分支節點，葉子節點組成。而每個分支節點也常常被稱作為一棵子樹。

• 根節點：二叉樹最頂層的節點

• 分支節點：除了根節點以外且擁有葉子節點

• 葉子節點：除了自身，沒有其他子節點

常用術語
在二叉樹中，我們常常還會用父節點和子節點來描述，比如圖中2為6和3的父節點，反之6和3是2子節點

二叉樹的三個性質

1. 在二叉樹的第i層上，至多有2^i-1個節點

• i=1時，只有一個根節點，2^(i-1) = 2^0 = 1

2. 深度為k的二叉樹至多有2^k-1個節點

• i=2時，2^k-1 = 2^2 - 1 = 3個節點

3. 對任何一棵二叉樹T，如果總結點數為n0，度為2(子樹數目為2)的節點數為n2,則n0=n2+1

樹和二叉樹的三個主要差別

• 樹的節點個數至少為1，而二叉樹的節點個數可以為0

• 樹中節點的大度數(節點數量)沒有限制,而二叉樹的節點的大度數為2

• 樹的節點沒有左右之分，而二叉樹的節點有左右之分

二叉樹分類

二叉樹分為完全二叉樹(complete binary tree)和滿二叉樹(full binary tree)

• 滿二叉樹：一棵深度為k且有2^k - 1個節點的二叉樹稱為滿二叉樹

• 完全二叉樹：完全二叉樹是指最后一層左邊是滿的，右邊可能滿也可能不滿，然后其余層都是滿的二叉樹稱為完全二叉樹(滿二叉樹也是一種完全二叉樹)

二叉搜索樹

二叉搜索樹滿足以下的幾個性質：

• 若任意節點的左子樹不空，則左子樹上所有節點的值均小于它的根節點的值；

• 若任意節點的右子樹不空，則右子樹上所有節點的值均大于它的根節點的值；

• 任意節點的左、右子樹也需要滿足左邊小右邊大的性質

我們來舉個例子來深入理解以下

一組數據：12,4,18,1,8,16,20
由下圖可以看出，左邊的圖滿足了二叉樹的性質，它的每個左子節點都小于父節點，右子節點大于其父節點，同時左子樹的節點都小于根節點，右子樹的節點都大于根節點

二叉搜索樹主要的幾個操作：

• 查找（search）

• 插入（insert）

• 遍歷（transverse）

二叉樹搜索樹的鏈式存儲結構

通過下圖，可以知道二叉搜索樹的節點通常包含4個域，數據元素，分別指向其左，右節點的指針和一個指向父節點的指針所構成，一般把這種存儲結構稱為三叉鏈表。

用代碼初始化一個二叉搜索樹的結點：

• 一個指向父親節點的指針 parent

• 一個指向左節點的指針 left

• 一個指向右節點的指針 right

• 一個數據元素，里面可以是一個key和value

    class BinaryTreeNode {
        constructor(key, value){
            this.parent = null;
            this.left = null;
            this.right = null;
            this.key = key;
            this.value = value;
        }
    }

接著我們再用代碼去初始化一個二叉搜索樹

• 在二叉搜索樹中我們會維護一個root指針，這個就相當于鏈表中的head指針，在沒有任何節點插入的時候它指向空，在有節點插入以后它指向根節點。

    class BinarySearchTree {
        constructor() {
            this.root = null;
        }
    }

創建節點

    static createNode(key, value) {
        return new BinarySearchTree(key, value);
    }

插入操作

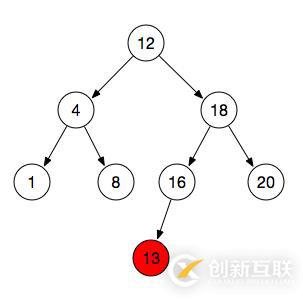
看下面這張圖，13是我們要插入的節點，它插入的具體步驟：

1. 跟根節點12做比較，比12大，所以我們確定了，這個節點是往右子樹插入的

2. 而根節點的右邊已經有節點，那么跟這個節點18做比較，結果小于18所以往18的左節點找位置

3. 而18的左節點也已經有節點了，所以繼續跟這個節點做比較，結果小于16

4. 剛好16的左節點是空的(left=null)，所以13這個節點就插入到了16的左節點

通過上面的描述，我們來看看代碼是怎么寫的

• 定義兩個指針，分別是p和tail，最初都指向root，p是用來指向要插入的位置的父節點的指針，而tail是用來查找插入位置的，所以最后它會指向null，用上圖舉個例子，p最后指向了6這個節點，而tail最后指向了null（tail為null則說明已經找到了要插入的位置）

• 循環，tail根據我們上面分析的一步一步往下找位置插入，如果比當前節點小就往左找，大則往右找，一直到tail找到一個空位置也就是null

• 如果當前的root為null，則說明當前結構中并沒有節點，所以插入的第一個節點直接為跟節點，即this.root = node

• 將插入后的節點的parent指針指向父節點

    insert(node){
        let p = this.root;
        let tail = this.root;
        
        // 循環遍歷，去找到對應的位置
       while(tail) {
            p = tail;
            // 要插入的節點key比當前節點小
            if (node.key < tail.key){
                tail.left = tail.left;
            }
            // 要插入的節點key比當前節點大
            else {
                tail.right = tail.right;
            }
        }
        
        // 沒有根節點，則直接作為根節點插入
        if(!p) {
            this.root = node;
            return;
        }
        
        // p是最后一個節點，也就是我們要插入的位置的父節點
        // 比父節點大則往右邊插入
        if(p.key < node.key){
            p.right = node;
        }
        // 比父節點小則往左邊插入
        else {
            p.left = node;
        }
        
        // 指向父節點
        node.parent = p;

    }

查找

查找就很簡單了，其實和插入差多，都是去別叫左右節點的大小，然后往下找

• 如果root = null, 則二叉樹中沒有任何節點，直接return，或者報個錯什么的。

• 循環查找

    search(key) {
        let p = this.root;
        if(!p) {
            return;
        }
        
       while(p && p.key !== key){
            if(p.key<key){
                p = p.right;
            }else{
                p = p.left;
            }
        }
        
        return p;
    }

遍歷

• 中序遍歷(inorder)：先遍歷左節點，再遍歷自己，最后遍歷右節點，輸出的剛好是有序的列表

• 前序遍歷(preorder)：先自己，再遍歷左節點，最后遍歷右節點

• 后序遍歷(postorder)：先左節點，再右節點，最后自己

最常用的一般是中序遍歷，因為中序遍歷可以得到一個已經排好序的列表，這也是為什么會用二叉搜索樹排序的原因

根據上面對中序遍歷的解釋，那么代碼就變的很簡單，就是一個遞歸的過程，遞歸停止的條件就是節點為null

• 先遍歷左節點-->yield* this._transverse(node.left)

• 遍歷自己 --> yield* node

• 遍歷左節點 --> yield* this._transverse(node.right)

    transverse() {
        return this._transverse(this.root);
    }
    
    *_transverse(node){
        if(!node){
            return;
        }
        yield* this._transverse(node.left);
        yield node;
        yield* this._transverse(node.right)
    }

看上面這張圖，我們簡化的來看一下，先訪問左節點4，再自己12，然后右節點18，這樣輸出的就剛好是一個12，4，8

補充：這個地方用了generater，所以返回的一個迭代器。可以通過下面這種方式得到一個有序的數組，這里的前提就當是已經有插入的節點了

   const tree = new BinaryTree();
   //...中間省略插入過程
    
   // 這樣就返回了一個有序的數組 
   var arr = [...tree.transverse()].map(item=>item.key);

完整代碼

class BinaryTreeNode {
  constructor(key, value) {
    // 指向父節點
    this.p = null;

    // 左節點
    this.left = null;

    // 右節點
    this.right = null;

    // 鍵
    this.key = key;

    // 值
    this.value = value;
  }
}

class BinaryTree {
  constructor() {
    this.root = null;
  }

  static createNode(key, value) {
    return new BinaryTreeNode(key, value);
  }

  search(key) {
    let p = this.root;
    if (!p) {
      return;
    }

   while (p && p.key !== key) {
      if (p.key < key) {
        p = p.right;
      } else {
        p = p.left;
      }
    }

    return p;
  }

  insert(node) {
    // 尾指針的父節點指針
    let p = this.root;

    // 尾指針
    let tail = this.root;

   while (tail) {
      p = tail;
      if (node.key < tail.key) {
        tail = tail.left;
      } else {
        tail = tail.right;
      }
    }

    if (!p) {
      this.root = node;
      return;
    }

    // 插入
    if (p.key < node.key) {
      p.right = node;
    } else {
      p.left = node;
    }

    node.p = p;
  }

  transverse() {
    return this.__transverse(this.root);
  }

  *__transverse(node) {
    if (!node) {
      return;
    }
    yield* this.__transverse(node.left);
    yield node;
    yield* this.__transverse(node.right);
  }
}

總結

二叉查找樹就講完了哈，其實這個和鏈表很像的，還是操作那么幾個指針，既然叫查找樹了，它主要還是用來左一些搜索，還有就是排序了，另外補充一下，二叉查找樹里找大值和最小值也很方便是不是，如果你大致讀懂了的話。

以上就是關于JavaScript二叉樹的詳細介紹，小編相信有部分知識點可能是我們日常工作會見到或用到的。希望你能通過這篇文章學到更多知識。更多詳情敬請關注創新互聯行業資訊頻道。

另外有需要云服務器可以了解下創新互聯scvps.cn，海內外云服務器15元起步，三天無理由+7*72小時售后在線，公司持有idc許可證，提供“云服務器、裸金屬服務器、高防服務器、香港服務器、美國服務器、虛擬主機、免備案服務器”等云主機租用服務以及企業上云的綜合解決方案，具有“安全穩定、簡單易用、服務可用性高、性價比高”等特點與優勢，專為企業上云打造定制，能夠滿足用戶豐富、多元化的應用場景需求。

網頁題目：關于JavaScript二叉樹的詳細介紹-創新互聯
分享路徑：http://www.yijiale78.com/article48/pihep.html

成都網站建設公司_創新互聯，為您提供網站策劃、網站設計公司、服務器托管、營銷型網站建設、企業網站制作、網站設計

廣告

聲明：本網站發布的內容（圖片、視頻和文字）以用戶投稿、用戶轉載內容為主，如果涉及侵權請盡快告知，我們將會在第一時間刪除。文章觀點不代表本網站立場，如需處理請聯系客服。電話：028-86922220；郵箱：631063699@qq.com。內容未經允許不得轉載，或轉載時需注明來源： 創新互聯